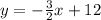So in the question we are given the points: (8,0) and (0,12)
In order to find the slope, we use the equation:
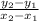
where subscripts 1 and 2 can apply to either of the points as long as they remain consistent. Let's use subscript 1 for the point (8,0) and subscript 2 for the point (0,12):
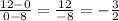
So now we know the slope of the equation is
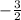 .
.
The slope-intercept form of a line follows the form:

where x and y are from a given point on the line, m is the slope of the line, and b is the y-intercept of the line.
So since we are told the y-intercept in the question, we can then plug in the numbers to the equation for the line: