Question

Match each value with its formula for ABC.

1.a/bxsinB
2.b/cxsinC
3.c/axsinA
4.sinA/sinCxc
5.sinB/sinAxa
6.sinC/sinBxb

Answer 1

1. sin A

2. sin B

3. sin C

4. a

5. b

6. c

Explanation:

According to the Law of sine

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

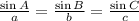
1.

`(\sin A)/(a)=(\sin B)/(b)`

`\sin A=(a)/(b)* \sin B`

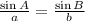
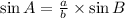
The of first formula is sin A.

2.

`(\sin B)/(b)=(\sin C)/(c)`

`\sin B=(b)/(c)* \sin C`

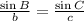
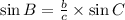
The of first formula is sin B.

3.

`(\sin A)/(a)=(\sin C)/(c)`

`(c)/(a)* \sin A=\sin C`

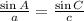
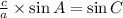
The of first formula is sin C.

4.

`(\sin A)/(a)=(\sin C)/(c)`

`(\sin A)/(\sin C)* c=a`

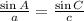
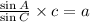
5.

`(\sin B)/(b)=(\sin A)/(a)`

`(\sin B)/(\sin A)* a=b`

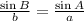
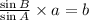
6.

`(\sin C)/(c)=(\sin B)/(b)`

`(\sin C)/(\sin B)* b=c`

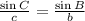
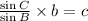
Therefore value of given formulas are sin A, sin B, sin C, a, b, c respectively.

Answer 2

For the triangle ABC use the sine theorem:

`(a)/(\sin A)= (b)/(\sin B)= (c)/(\sin C)`.

1. From
`(a)/(\sin A)= (b)/(\sin B)` you have
`(a)/(b) \cdot \sin B=\sin A`.

2. From
`(b)/(\sin B)= (c)/(\sin C)` you have
`(b)/(c) \cdot \sin C=\sin B`.

3. From
`(a)/(\sin A)= (c)/(\sin C)` you have
`(c)/(a) \cdot \sin A=\sin C`.

4. From
`(a)/(\sin A)= (c)/(\sin C)` you have
`(\sin A)/(\sin C) \cdot c=a`.

5. From
`(a)/(\sin A)= (b)/(\sin B)` you have
`(\sin B)/(\sin A) \cdot a=b`.

6. From
`(b)/(\sin B)= (c)/(\sin C)` you have
`(\sin C)/(\sin B) \cdot b=c`.