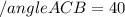Question

`stackrel(harr)(DG)` and `stackrel(harr)(EG)` are tangent to circle C and circle F. The points of tangency are A, B, D, and E. If m`/_DFE` = 140°, what is m`/_ACB`?

Answer 1

The correct answer is B. 140

Answer 2

General Idea:

Sum of angles subtended at the centre and point of contact by tangents down from an external point is supplementary (180°).

Applying the concept:

Considering the point of contact of two tangents of large circle, we can write

`\angle DFE+\angle DGE=180`

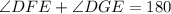
We are given
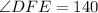`\angle DFE=140`, so the equation will become

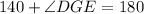`140+\angle DGE=180` {Subtracting 140 on both sides}

`140+\angle DGE -140 = 180 - 140\\ \\ \angle DGE = 40`

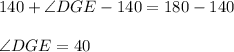
Considering the point of contact of two tangents of small circle, we can write

`\angle ACB + \angle AGB = 180\\ \\ Note: \angle AGB = \angle DGE = 40\\ \\ \angle ACB + 40 = 180`

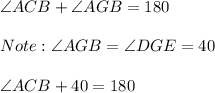
Subtracting 40 on both sides, we get...

`\angle ACB +40 - 40 = 180 - 40\\ \\ \angle ACB = 140`

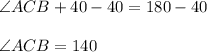
Conclusion:

`/angle ACB = 40`