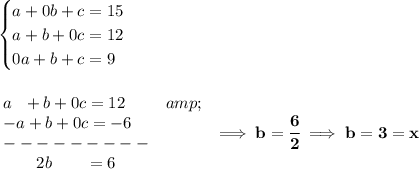check the picture below.
as you know, two tangent lines to the same circle, when they meet, their length is the same, therefore, as you see in the picture, a = a, b = b, c = c, those tangents are three twins.
also recall that the point of tangency, where the radius touches the tangent line, is always a right-angle, as you see there.
and we know the lengths of a + c = 15, a + b = 12 and b + c = 9.
we can write them as a system of equations of 3 variables, and we'll do some elimination, so let's proceed.
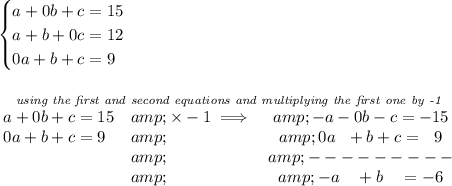
which we can again write it as -a + b + 0c = -6.
and now, let's use that resultant equation and use it with the second equation as is