Question

The area of the region under the curve given by the function f(x) = 2x2 + 6 on the interval [0, b] is 36 square units, where b > 0.

What is the value of b?

Answer 1

The area as a function of b is given by

`a(b)=\int\limits^b_0 {(2x^2+6)} \, dx =(2)/(3)b^3+6b`

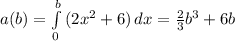
You want to find b such that a(b) = 36.

... (2/3)b^3 +6b = 36

... b^3 +9b -54 = 0 . . . . multiply by 3/2 to clear fractions

A graphing calculator shows this equation to have one real solution at b=3.

The value of b is 3.