Question

Explain why the two figures below are not similar. Use complete sentences and provide evidence to support your explanation.

Answer 1

So with similar figures, the corresponding sides will all be proportional. But before I can use ratios, I have to use the distance formula,
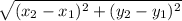`√((x_2-x_1)^2+(y_2-y_1)^2)` on BC and IJ.

B = (-3,0)

C = (-1,1)

`√((-1-(-3))^2+(1-0)^2)`

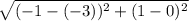
Firstly, solve the parentheses:
`√((2)^2+(1)^2)`

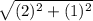
Next, solve the exponents:
`√(4+1)`

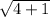
Next, solve the addition, and your answer will be √5.

(The process with IJ will be similar, so I'll just go through it real quickly.)

I = (5,0)

J = (6,1)

`√((6-5)^2+(1-0)^2)\\ √((1)^2+(1)^2)\\ √(1+1)\\ √(2)`

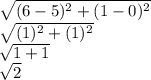
Now we can do the ratios:

`(BC)/(IJ) =(CD)/(JK) =(DE)/(KL) =(EF)/(LM) =(FG)/(MN) =(GA)/(NH) =(AB)/(HI)\\ (√(5))/(√(2))=(4)/(2) =(2)/(1) =(2)/(1) =(1)/(1) =(4)/(2) =(2)/(1)`

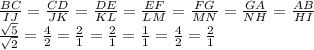
From the ratios above, we can see that the sides are all not proportionally the same, therefore these figures are not similar.