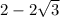The quadratic formula states that the solutions to the equation
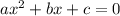 are (if they exist)
are (if they exist)
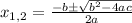
In your case, the quadratic equation is identified by the choice
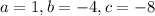 , and this leads to the solutions
, and this leads to the solutions
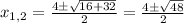
Since
 , we have
, we have

So, the expression for the solutions becomes
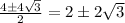
So, the two solutions are
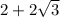 and
and