Question

The center of a hyperbola is located at the origin. One focus is located at (−50, 0)

Answer 1

An hyperbola looks sort of like two mirrored parabolas, with the two "halves" being called "branches".

The equation of hyperbola is:
`((x-h)^(2))/(a^(2)) -((y-k)^(2))/(b^(2)) =1`

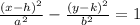
As, Center is origin or (0,0). The equation becomes:
`(x^(2))/(a^(2)) -(y^(2))/(b^(2)) =1`

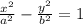
As one focus is (-50,0). So, the other focus is (50,0). (As shown in diagram)