Question

URGENT PLEASE HELP WITH MATH

Ariana has $4 to spend at the candy shop. She wants at least 10 sour snaps which are 15 cents each, and at least 3 chocolate truffles which are 80 cents each. Which of the following systems of inequalities correctly represents the constraints on the variables in this problem? Let s represent the sour snaps and t represent the chocolate truffles.

A .15s + .80t < 4
s>10
t>3

B. 10s+3t>4
s<15
t<80

C. 10s+3t <4
s>15
t>80

D. .15s+80t>4
s<10
t<3

Answer 1

Let s represent the sour snaps and t represent the chocolate truffles.

OK, got it. s is the number of snaps and t the number of truffles.

She wants at least 10 sour snaps.

We write that as

`s \ge 10`

and at least 3 chocolate truffles

`t \ge 3`

Ariana has $4 to spend at the candy shop.

sour snaps which are 15 cents each,

chocolate truffles which are 80 cents each.

We can write our equation in dollars or cents. Let's do it both ways, dollars first. 0.15 s is the dollar amount spent on snaps, 0.80 t the dollar amount spent on truffles.

`0.15 s + 0.80 t \le 4`

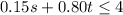
In cents, that's the equivalent

`15 s + 80 t \le 400`

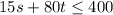
Which of the following systems of inequalities correctly represents the constraints on the variables in this problem?

Really none of the above because they're written with less than and greater than rather than our correct less than or equal to and greater than or equal to signs. I'll add the = and answer the problem that way.

A .15s + .80t <= 4

s>=10

t>=3

B. 10s+3t>=4

s<=15

t<=80

C. 10s+3t <=4

s>=15

t>=80

D. .15s+80t>=4

s<=10

t<=3

Choice A (suitably edited) agrees with what we got

Answer: A

Answer 2

The most she has to spend is $4 so the total coat of candy has to be less than $4

The cost of a sour snap is 15 cents which is 0.15

so a sour snap would be 0.15s

The cost of a chocolate truffle is 80 cents, which is 0.80

so a chocolate truffle would be 0.80t

The equation would be 0.15S + 0.80t < 4

with S > 10 and t>3

The correct answer is A.