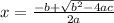Question

Describe how to derive the quadratic formula from a quadratic equation in standard form

Answer 1

The quadratic formula is derived from a quadratic equation in standard form when solving for x by completing the square. The steps involve creating a perfect square trinomial, isolating the trinomial, and taking the square root of both sides. The variable is then isolated to give the solutions to the equation.

Explanation:

:)

Answer 2

Firstly we learn the standard quadratic equation,

ax²+bx+c=0

where a,b,c are real numbers.

Now solve the quadratic equation using the Complete the square method.

Rewriting part of the equation as a perfect square trinomial. If you complete the square on the generic equation ax² + bx + c = 0 and then solve for x,

ax²+bx=-c

x² +
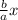`(b)/(a) x`=-c

add both the side
`((b)/(2a) )^(2)`

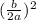
x² +
`(b)/(a) x`+
`((b)/(2a))^(2) = -(c)/(a) + ((b)/(2a))^(2)`

`(x+(b)/(2a))^(2) = (b^(2)-4ac)/(4a^(2))``

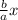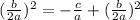
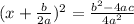take square root both the side

`x = \frac{-b+\sqrt{b^(2)-4ac}}{2a}`

`x= \frac{-b-\sqrt{b^(2)-4ac}}{2a}`