Question

The benzoate ion, c6h5coo− is a weak base with kb=1.6×10−10. how many moles of sodium benzoate are present in 0.50 l of a solution of nac6h5coo if the ph is 9.04?

Answer 1

Answer : The number of moles of sodium benzoate is, 0.375 moles

Solution :

First we have to calculate the pOH.

`pOH=14-pH=14-9.04=4.96`

Now we have to calculate the concentration of [tex[OH^-[/tex] ions.

`pOH=-\log [OH^-]`

`4.96=-\log [OH^-]`

`[OH^-]=1.096* 10^(-5)`

The equilibrium reaction for dissociation of weak base is,

`C_6H_5COO^-+H_2O\rightleftharpoons OH^-+C_6H_5COOH`

initially conc. c 0 0

At eqm.
`c(1-\alpha)`
`c\alpha`
`c\alpha`

The expression for dissociation constant is,

`k_b=(c\alpha* c\alpha)/(c(1-\alpha))`

when
`\alpha` is very very small the, the expression will be,

`k_b=(c^2\alpha^2)/(c)=c\alpha^2\\\\\alpha=\sqrt{(k_b)/(c)}`

And,

`[OH^-]=c\alpha`

Thus the expression will be,

`[OH^-]=√(k_b* c)`

Now put all the given values in this expression, we get

`1.096* 10^(-5)=\sqrt{(1.6* 10^(-10))* c}`

`c=0.75M`

Now we have to calculate the moles of sodium benzoate.

`Moles=concentration* volume=0.75M* 0.5L=0.375moles`

Therefore, the number of moles of sodium benzoate is, 0.375 moles

Answer 2

`NaC6H5COO \rightarrow Na{^(+)} + C6H5COO^(-)`

Here the base is a benzoate ion, which is a weak base and reacts with water.

`C6H5COO^(-)(aq) + H2O (l)\leftrightarrow C6H5COOH(aq)+ OH^(-)(aq)`

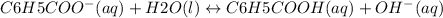
The equation indicates that for every mole of OH- that is produced , there is one mole of C6H5COOH produced.

Therefore [OH-] = [C6H5COOH]

In the question value of PH is given and by using pH we can calculate pOH and then using pOH we can calculate [OH-]

pOH = 14 - pH

pH given = 9.04

pOH = 14-9.04 = 4.96

pOH = -log[OH-] or
`[OH^(-)] = 10^{^(-pOH)}`

`[OH^(-)] = 10^{^(-4.96)}`

`[OH^(-)] = 1.1* 10^(-5)`

The base dissociation equation kb =
`(Product)/(Reactant)`

`kb =([C6H5COOH][OH^(-)])/([C6H5COO^(-)])`

H2O(l) is not included in the 'kb' equation because 'solid' and 'liquid' are taken as unity that is 1.

Value of Kb is given =
`1.6* 10^(-10)`

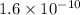
And value of [OH-] we have calculated as
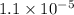`1.1* 10^(-5)` and value of C6H5COOH is equal to OH-

Now putting the values in the 'kb' equation we can find the concentration of C6H5COO-

`kb =([C6H5COOH][OH^(-)])/([C6H5COO^(-)])`

`1.6* 10^(-10) = ([1.1* 10^(-5)][1.1* 10^(-5)])/([C6H5COO^(-)])`

`[C6H5COO^(-)] = ([1.1* 10^(-5)][1.1* 10^(-5)])/(1.6* 10^(-10))`

`[C6H5COO^(-)] = 0.76 M` or
`0.76(mol)/(L)`

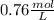
So, Concentration of NaC6H5COO would also be 0.76 M and volume is given to us 0.50 L , now moles can we calculated as : Moles = M X L

Moles of NaC6H5COO would be =
`0.76((mol)/(L)) * (0.50L)`

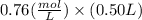
Moles of NaC6H5COO (sodium benzoate) = 0.38 mol