Question

Plsss answer the following.

Answer 1

First exercise:

a. The first prime numbers are 2,3,5,7,11,... So, the greatest prime interger between 4 and 9 is 7. A = 7.

b. Since the number line's growing direction is rightwards, going to the left means to decrease. So, point E is 4 less than point A, i.e. 7-4 = 3. E = 3.

c. The additive inverse of a number
`x` is another number
`y` such that
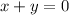`x+y=0`. So, we're looking form a number such that
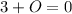`3+O=0`, and thus O = - 3.

d. This point looks a bit ambiguous to me honestly. We know that IO = 2, which I presume means that the points I and O are two units apart, but we're not told if I is two units left or right with respect to O. To solve this issue, I'm assuming that IO implies that I sits before O, and so I is two units left with respect to O. As we said in point a., two units left means two less, so we have I = -3-2 = -5. At this point, point L is halfway between -5 and -3, and thus L = - 4.

e. The sum of the coordinates of A and E is 7 + 3 = 10. Half that sum is 5, so M = 5.

In the attached image, you can see the number line filled with the points asked by the exercise.

Second exercise:

All the requests can be written as an equation in which we look for the values of x. Below you find the equation and the solutions.


`107 + x = 55 \implies x = 55-107 = -52`


`-43 - x = 18 \implies x = -43-18 = -61`


`-43 - x = 18 \implies x = -43-18 = -61`


`55x = 0 \implies x = (0)/(55) = 0`


`(x)/(-1080) = -40 \implies x = (-1080)(-40) = 43200`

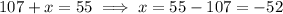
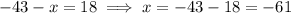
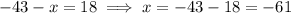
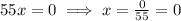
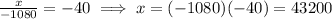
A little side note: I've honestly never met the expression "subtract A to B", but always "subtract A from B". I assumed they mean the same thing, but if anybody thinks I'm wrong please let me know! (I'm not a native speaker, so I can only refer to the math I met during my studies).