Question

Two blocks on a frictionless horizontal surface are on a collision course. one block with mass 0.6 kg moves at 0.8 m/s to the right and collides with a 1.2 kg mass at rest and the two masses bounce off each other elastically. find the final velocities of the two masses after the collision.

Answer 1

First we can say that since there is no external force on this system so momentum is always conserved.

`m_1v_(1i) + m_2v_(2i) = m_1v_(1f) + m_2v_(2f)`

`0.6*0.8 + 1.2*0 = 0.6*v_(1f) + 1.2*v_(2f)`

`0.48= 0.6*v_(1f) + 1.2*v_(2f)`

`0.8 = v_(1f) + 2v_(2f)`

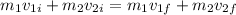
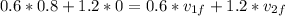
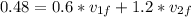
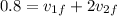
now by the condition of elastic collision

`v_(2f) - v_(1f) = 0.8 - 0[\tex]</p><p>now add two equations</p><p>[tex]3*v_(2f) = 1.6`

`v_(2f) = 0.533 m/s`

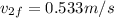
also from above equation we have

`v_(1f) = -0.267 m/s`

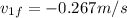
So ball of mass 0.6 kg will rebound back with speed 0.267 m/s and ball of mass 1.2 kg will go forwards with speed 0.533 m/s.