Answer : option D
The rate of change is not constant and increases then decreases over time. The height of the ball above ground gets larger until 1.25 seconds and then gets smaller after that time.
Rate of change is nothing but the slope
To find slope we use formula
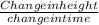
Time (seconds) Height (feet) Rate of change
0 -------------------------0
0.5 -----------------------16 --------------------
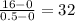
1 ----------------------24 --------------------
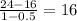
1.25 -----------------------25--------------------

1.5 -------------------------24 --------------------
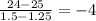
2 ----------------------------16 --------------------

2.5 -------------------------0 --------------------
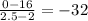
Rate of change is positive till 1.25 seconds and then it becomes negative. From this it is clear that, the rate of change is not constant and increases then decreases over time. The height of the ball above ground gets larger until 1.25 seconds and then gets smaller after that time.