Question

Three ships, A, B, and C, are anchored in the atlantic ocean. The distance from A to B is 36.318 miles, from B to C is 37.674 miles, and from C to A is 11.164 miles. Find the angle measurements of the triangle formed by the three ships.

Answer 1

Let us draw the triangle

here the sides a= 37.674 miles

b= 11.164 miles

c= 36.318 miles

Lets use the cosine rule to solve for the angles

( we cannot use the sine law since we do not have the measure of any of the angles)

The cosine law

`c^(2) = a^(2) +b^(2) -2ab cos C`

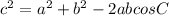
Let us plug in the values

`(36.318)^(2) = (37.674)^(2) + (11.164)^(2) - 2(37.674)(11.164). Cos C`

`1318.997 = 1419.33 + 124.634 - 841.184. Cos C`

`1318.997 = 1543.964 - 841.184. Cos C`

`841.184. Cos C = 1543.964-1318.997`

`841.184. Cos C = 224.967`

`Cos C = (224.967)/(841.184)`

`cos C = 0.267`

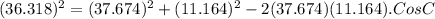
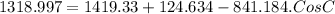
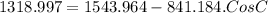
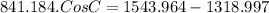
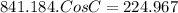
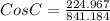
C = 74.48°

We can use the sine law to calculate the value of angle A

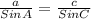
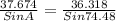
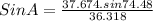
`(a)/(SinA) = (c)/(Sin C)`

`(37.674)/(Sin A) = (36.318)/(Sin 74.48)`

`Sin A = (37.674. sin 74.48)/(36.318)`

`Sin A = (37.674 X 0.963)/(36.318)`

`Sin A = 0.998`

A=
`sin^(-1) (0.998)`

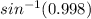
A = 87.38°

Now we can easily find the third angle B by subtracting angle A and C from 180°

`B = 180-(74.48 + 87.38)`

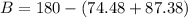
B = 180-161.86

B = 18.14°

Hence we have all the three angles ( attached figure)