Question

1 kg of ice at 0° c is mixed with 9 kg of water at 50° c (the latent heat of ice is 3.34x105 j/kg and the specific heat capacity of water is 4160 j/kg). what is the resulting temperature?

Answer 1

The final temperature of the mixture is 46.2°C.

According to the theory of heat exchange, heat absorbed by ice is equal to the heat given by water. Ice absorbs heat to first melt at a constant temperature of 0°C and then water at 0°C increases its temperature to the final temperature T. The amount of heat for this process is provided by hot water at 50°C, which cools down to the final temperature of the mixture T.

Heat absorbed by ice is given by,
`[tex] Q_(a) =m_(ice) *L+m_(ice)*c_(w) (T-0)`
=(1 kg)(3.34*10^5 J/K)+(1 kg)(4160 J/kg)(T-0)
=3.34*10^5+4160T
[/tex]

heat given by water is given by

`image`

Equating both the equations and solving for T,

°
`image`

Answer 2

ice:

mass (m) = 1 kg

Initial Temperature (T) = 0 ° C

Latent heat (L) = 3.34 * 105 J/kg

Water:

mass (m) = 9 kg

Initial Temperature (T) = 50 ° C

Specific heat capacity (c) = 4,160 J/kg

First you must find the amount of heat required for the ice to turn into water (Q is heat)

Q = mL

Q = 1 * ( 3.34 *
`10^(5)`)

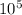Q = 3.34 *
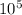`10^(5)` J

1 kg of ice needs 3.34 * J of energy to convert into water

The heat lost by the water is equal to the heat gained by the ice.

Heat can be found using the equation: Q = mcΔT therefore...

mcΔT (water) = mcΔT (ice)

9 * 4,160(50 - x) = 1 * 4,160(x - 0) + 3.34 *
`10^(5)`

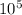
You need to add the heat needed for the ice to convert into the water (3.34 *
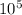`10^(5)` J) to the ice side of the equation, because when we get the final temperature the ice will be converted into water.

x = 36.97

The resulting temperature is 36.97 ° C

I hope this helped!

~Just a girl in love with Shawn Mendes