Question

Determine which of the following statements are true if Parabola 1 has the equation f(x)=x^2-4x-12 and Parabola 2 has a leading coefficient of 1 and zeros at x = 4 and x = -2. Check all that apply.

A. Parabola 1 has a lower minimum than Parabola 2.
B. Parabola 1 crosses the y-axis higher than Parabola 2.
C. Parabola 1 and Parabola 2 have the same line of symmetry.
D. Parabola 1 and Parabola 2 have a zero in common.

Answer 1

the correct answers are

Parabola 1 and Parabola 2 have a zero in common.

Parabola 1 has a lower minimum than Parabola 2.

Answer 2

First of all, we have to find Parabola 2. The general formula is

`g(x) = ax^(2) +bx+c`.

It is given that the leading coefficient is 1, then a=1. Putting 4 and -2 into the formula, we have to solve the following system of equations:

`\left \{ {{16+4b+c=0} \atop {4-2b+c=0}} \right.`

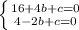
Solving it, we find that b=-2 and c=-8

Parabola 2 is given with

`g(x)=x^(2) -2x-8`

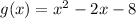
Both functions have a minimum because the parabolas located upwardly. The minimum of Parabola 1 is located below the minimum of Parabola 2. You can observe this result in the attached picture, as well. Parabola 1 is given with blue line.