Question

The length of the arc intercepted by a congruent central angle is proportional to the _______ in similar circles.

Answer 1

Answer :The length of the arc intercepted by a congruent central angle is proportional to the radius in similar circles.

Lets assume two concentric circles with same center.(refer attached figure)

The two slices are in proportion.

From the similar slices , the corresponding parts are in proportion

S1, S2 are the arc length

r1,r2 are the radius

`(S1)/(S2)` =
`(r1)/(r2)`

The proportion can be written as

`(S1)/(r1)` =
`(S2)/(r2)`

This ratio shows that the arc length intercepted by a congruent central angle is proportional to the radius in similar circles.

Answer 2

Please find the attachment for a better understanding of the answer.

As we can clearly see from the diagram, as the radius of the circle reduces so does the length of the arc for the same congruent angle subtended at the center.

Thus the length of the arc intercepted by a congruent central angle is proportional to the radius in similar circles.

This can be mathematically proven as thus:

Let
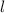`l` be the length of the arc

Let theta be the central angle

Let r be the radius.

We know that
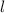`l`=(theta)r

Therefore, for a constant theta, the arc length will vary in the same proportion as the radius.