Question

Landon is standing in a hole that is 5.1 ft deep. He throws a rock, and it goes up into the air, out of the hole, and then lands on the ground above. The path of the rock can be modeled by the equation y = -0.005x^2 + 0.41x - 5.1, where x is the horizontal distance horizontal distance of the rock, in feet, from Landon and y is the height, in f of the rock, in feet, from Landon and y is the height, in feet, of the rock above the ground. How far horizontally from Landon will the rock land? 33.35 ft 66.71 ft 7.65 ft 15.29 ft

Answer 1

When the rock lands on the ground, it has no height. Or you could say that it has a height of 0. Therefore, our equation when the height, y, is 0, looks like this:
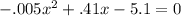`-.005x^2+.41x-5.1=0`. Where the height is 0 is where the quadratic goes through the x axis. To find those places where the graph goes through the x-axis, or where the rock hits the ground, x, we have to factor that quadratic to solve for x. Fit that into the quadratic formula to find that x = 15.29 and x = 66.71. These 2 points are the x-intercepts. Because Landon is below the ground, which also happens to be below the first x-intercept, this means that when he throws the rock it goes UP through x = 15.29, up to its highest point (the vertex), and then lands at the other x-intercept, which is 66.71. The x values are where the ROCK is at ground level, not Landon. So your answer is 66.71.