Question

How to resolve this?
Thank you

Answer 1

Serious stuff for July.

1. Sum of n even squares.

This is related to the sum of the squares of the integers. Lots of different proofs; how about we start from the difference of consecutive cubes.

`\displaystyle S = \sum_(k=1)^n ((k+1)^3 - k^3)`

`\displaystyle S = \sum_(k=1)^n (3k^2 + 3k + 1)`

`\displaystyle S = 3 \sum k^2 + 3 \sum k + \sum 1`

`\displaystyle S = 3 \sum k^2 + 3n(n+1)/2 + n`

`\displaystyle \sum k^2 = \frac 1 3(S - (3/2) n(n+1) - n)`

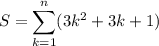
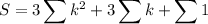
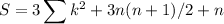
So all we need is S which is nicely telescoping:

`S = (2^3 - 1^3) + (3^2 - 2^3) + (4^3 - 3^3) + ... + (n+1)^3-n^3`

`S = (n+1)^3 - 1`

`\displaystyle \sum k^2 = \frac 1 3((n+1)^3 - 1 - (3/2) n(n+1) - n)`

`\displaystyle \sum k^2 = \frac 1 6 n (n + 1) (2 n + 1)`

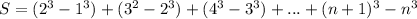
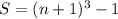
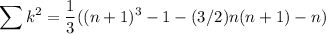
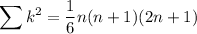
We're interested in

`\displaystyle \sum (2k)^2 = 4 \sum k^2 = \frac 2 3 n (n + 1) (2 n + 1) \quad\checkmark`

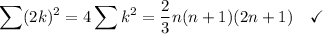
That's just the first one. This is gonna be a long problem set.

2.

`\displaystyle S = \sum_(j=1)^n (3j - 2)`

That's a lot easier.

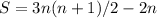
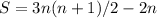
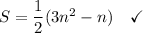
`\displaystyle S = 3 \sum j - \sum 2`

`S = 3n(n+1)/2 - 2n`

`S = 3n(n+1)/2 - 2n`

`S = \frac 1 2 (3n^2 -n) \quad\checkmark`

3.

`\displaystyle \sum_(k=1)^n (5k-1) = 5 \sum k - \sum 1 = \frac 5 2 n(n+1)-n = \frac n 2(5n+3) \quad\checkmark`

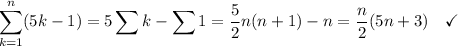
4.

Now it's getting interesting again.

`\displaystyle S=\sum_(p=1)^n p(2^(p-1))`

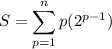
If I recall, the trick with these is turning them into double sums. Instead of multiplying by p, we'll add up p times.

`\displaystyle S=\sum_(p=1)^n \sum_(q=1)^p 2^(p-1)`

Let's just look at this for a minute as

`\displaystyle S=\sum_(p=1)^n \sum_(q=1)^p f(p) = f(1) + f(2)+f(2) + f(3)+f(3)+f(3)+...`

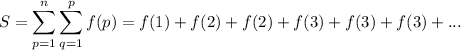
This is the tricky part; we want to exchange the order of the sums but we have the outer index p in the inner bound. When q is the outer sum it can't go to p so it must go to n:

`\displaystyle S=\sum_(q=1)^n \sum_(p=?)^? f(p)`

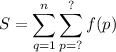
We have to fill in the question marks. We need
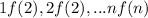`1f(2), 2f(2), ...nf(n)` so we can see the bounds are:

`\displaystyle S=\sum_(q=1)^n \sum_(p=q)^n f(p)`

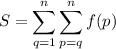
We can write the sum as the difference of two sums from 1.

`\displaystyle S= \sum_(q=1)^n \left(\sum_(p=1)^n f(p) - \sum_(p=1)^(q-1) f(p) \right)`

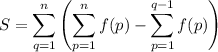
OK we substitute back in for f.

`\displaystyle S=\sum_(q=1)^n \left( \sum_(p=1)^n 2^(p-1) - \sum_(p=1)^(q-1) 2^(p-1) \right)`

That's two geometric series

`\displaystyle S=\sum_(q=1)^n ( (1-2^n)/(1-2) - (1-2^(q-1))/(1-2) )`

`\displaystyle S=\sum_(q=1)^n ( 2^n - 2^(q-1))`

`\displaystyle S=\sum_(q=1)^n 2^n - \sum_(q=1)^n 2^(q-1)`

`\displaystyle S=n 2 ^n - (1-2^n)/(1-2)`

`\displaystyle S = (n-1)2^n + 1 \quad\checkmark`

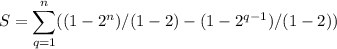
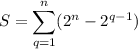
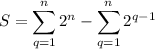
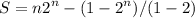
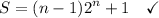
5.

`\displaystyle S = \sum_(k=1)^n (1)/(k^2 + k)`

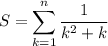
Hmmm. Looks complicated but is that just a telescoper?

`\displaystyle S = \sum_(k=1)^n (1)/(k(k+1))`

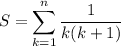
It's not too hard to just guess the partial fractions:

`\displaystyle S = \sum_(k=1)^n \left((1)/(k) - (1)/(k+1)\right)`

`\displaystyle S = (1)/(1) - (1)/(2) + (1)/(2) - (1)/(3) + ... + (1)/(n) - (1)/(n+1)`

`\displaystyle S = 1 - (1)/(n+1)`

`\displaystyle S = (n)/(n+1) \quad\checkmark`

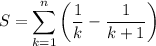
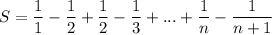
Phew. Tough problem set. It occurs to me now we could have done the hard ones by induction which probably would have been simpler.