Answer:
The reflection image would be (-6,8).
Explanation:
Since, when a point is reflected across a line x = p
Then, the rule of reflection is,
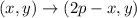
While, across a line y = p,
The rule of reflection is,
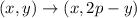
Thus, when (0,0) is reflected across x = -3,
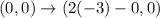
The image after reflection is (-6,0),
Again when (-6,0) is reflected across y = 4,
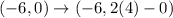
Hence, the resultant image after both reflections would be (-6,8).