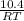The correct ratios are: cse 27=23/RT, sec 27= 23/10.4 and cot 63 = RT/10.4
In triangle RST, angle T= 90° and angle R= 63°
As the total of all angle in any triangle is 180°, so the measure of the angle S = 180°- (90°+63°)
S= 180°- 153°
S= 27°
According to the rule of trigonometric ratios,
cse(θ) =
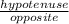
sec(θ) =
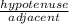
cot(θ) =
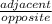
In respect of angle R (63°), side RS(23) is hypotenuse , ST(10.4) is opposite and RT is adjacent.
So, cse(63°) =
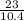
sec(63°) =
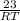
cot(63°) =
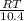
Now, in respect of angle S(27°), hypotenuse is RS(23), adjacent is ST(10.4) and opposite is RT.
So, cse(27°) =
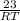
sec(27°) =
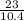
cot(27°) =