In the population growth formula, P is the final population, A is the initial population, e is euler's number, k is the growth constant, and t is the time in years. We have enough information to solve for k given what we have for the years 91 and 2000. Our P is going to be the population in 2000, our A is going to be the population in 1991, and t is the difference between them, which is 9. We set up to solve for k:
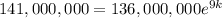 . We divide those 2 huge numbers to get
. We divide those 2 huge numbers to get
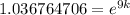 . In order to get that k out from its current place as an exponent, we have to take the natural log of both sides. Since the natural log has a base of e, taking the natural log of e undo each other, leaving us with
. In order to get that k out from its current place as an exponent, we have to take the natural log of both sides. Since the natural log has a base of e, taking the natural log of e undo each other, leaving us with
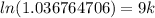 . On our calculator we find that natural log of that decimal is .0361050048, so our equation now looks like this:
. On our calculator we find that natural log of that decimal is .0361050048, so our equation now looks like this:
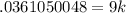 . Dividing by 9 we have a k value that is very tiny at .0040116672. Now we can use that in our equation to find the population estimation in 2016. Our P is our unknown, our A is the same as before at 136,000,000; and our t is the difference between 2016 and 1991, which is 25. Setting up to solve for P this time:
. Dividing by 9 we have a k value that is very tiny at .0040116672. Now we can use that in our equation to find the population estimation in 2016. Our P is our unknown, our A is the same as before at 136,000,000; and our t is the difference between 2016 and 1991, which is 25. Setting up to solve for P this time:
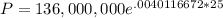 , which simplifies to
, which simplifies to
 . First we raise e to that decimal on our calculator and then multiply it by the 136,000,000 to get an estimation of population to be 150,347,091. They want that rounded to the neasrest million, so the final answer will be 150,000,000
. First we raise e to that decimal on our calculator and then multiply it by the 136,000,000 to get an estimation of population to be 150,347,091. They want that rounded to the neasrest million, so the final answer will be 150,000,000