Question

Which function represents a translation of the parent cubic function 8 units to the left? h(x) = x3 + 8 h(x) = x3 – 8 h(x) = (x + 8)3 h(x) = (x – 8)3

Answer 1

h(x)=(x+8)3

Explanation:

Answer 2

Using the definition of the Vertical shifts of graphs of the function :

"Suppose c>0,

To graph y=f(x)+c, shift the graph of y=f(x) upward c units.

To graph y=f(x)-c, shift the graph of y=f(x) downward c units"

Again we recall the definition of Horizontal shifts of graphs:

" suppose c>0,

the graph y=f(x-c), shift the graph of y=f(x) to the right by c units

the graph y=f(x+c), shift the graph of y=f(x) to the left by c units. "

consider
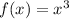`f(x)=x^3` is the parent function.

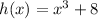`h(x)=x^3+8` shifts the graph
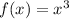`f(x)=x^3` upward by 8 units

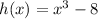`h(x)=x^3-8` shifts the graph
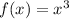`f(x)=x^3`downward by 8 units

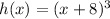`h(x)=(x+8)^3` shifts the graph
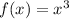`f(x)=x^3` left by 8 units

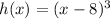`h(x)=(x-8)^3` shifts the graph
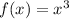`f(x)=x^3` right by 8 units.