Question

For f(x) = 0.01(2)x, find the average rate of change from x = 2 to x = 10. 1.275 8 10.2 10.24

Answer 1

The average rate of change of f(x) from x=2 to x=10 is:

1.275

Explanation:

The average rate of change of a function f(x) from x=a to x=b is given by the formula:

`Rate\ of\ change=(f(b)-f(a))/(b-a)`

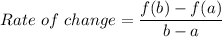
The function f(x) is given by:

`f(x)=0.01\cdot 2^x`

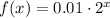
We need to find the average rate of change of f(x) from x=2 to x=10

Hence, the average rate of change is calculated by:

`Rate\ of\ change=(f(10)-f(2))/(10-2)\\\\i.e.\\\\Rate\ of\ change=(0.01\cdot 2^(10)-0.01\cdot 2^2)/(8)\\\\Rate\ of\ change=(0.01* 2^2(2^8-1))/(8)\\\\i.e.\\\\Rate\ of\ change=(0.01* 255)/(2)\\\\Rate\ of\ change=1.275`

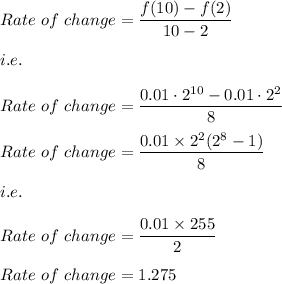
Hence, the answer is: 1.275

Answer 2

The average rate of change is ...

... (change in f(x))/(change in x)

... = (f(10) - f(2))/(10 - 2)

... = (10.24 - 0.04)/8 = 10.2/8 = 1.275