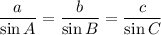You mean Lami’s Theorem?
Consider the figure. Three concurrent forces net to static equilibrium at the origin. Let's assume for simplicity force a is along the positive x axis.
We have equilibrium when the components of force balance in both dimensions. In particular in the y dimension,
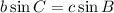
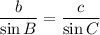
We're free to move our coordinate system around to make any of the force vectors the x axis and then we'd get the same sine balance as in the Law of Sines for the remaining pair of sides.