The sum of the inner angles of any triangle is always 180°, i.e. you have
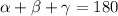
In the particular case of an equilater triangle, all three angles are the same, so
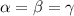
and the expression becomes
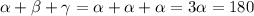
which implies
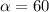
So, if you rotate the triangle with respect to its center by 60 degrees, the triangle will map into itself. In particular, if you want point A to be mapped into point B, you have to perform a counter clockwise rotation of 60 degrees with respect to the center of the triangle.
Of course, this is equivalent to a clockwise rotation of 120 degrees.
Finally, both solutions admit periodicity: a rotation of 60+k360 degrees has the same effect of a rotation of 60 degrees, and the same goes for the 120 one (actually, this is obvisly true for any rotation!)