Question

Write an equation that has a hole at x = 2, a hole at x = 0 and a vertical asymptote at x = 1.

Thank you!! Please reply I really don't understand how to do this and my grade depends on this

Answer 1

Anytime you have a hole in a rational function, it means that both the numerator and denominator must have zero as that value. So if the hole is at x = 2, it means that when you evaluate the rational function at 2, there's going to be a zero in the numerator and denominator.

What makes it so that when evaluate at 2 to get a zero? x - 2. This comes from x = 2 and subtracting 2 from both sides. Put 2 into x-2 and we get the zero we want. So
`(x-2)/(x-2)` must be in the function.

The next discontinuity is a hole at zero. That's the same process as above, and x will work. Put in 0, get 0 back. So
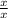`(x)/(x)` must be there too. We are going to MULTIPLY both pieces we have so we make sure both are there.

Lastly is the vertical asymptote at x = 1. The denominator must be zero, the numerator here can be anything. We set x = 1 equal to zero and subtract one from both sides to give x-1. Our function needs
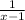`(1)/(x-1)` to include the asymptote. We use a 1 here because it's just a placeholder. Any number would work or any variable would work as long as it wasn't x-1.

Now we put them together and MULTIPLY all the pieces.

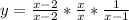`y = (x-2)/(x-2) * (x)/(x) * (1)/(x-1)` has all the pieces - the hole at 2, the hole at 0, and the vertical asymptote at 1. (We can multiply all the pieces out if we want).