Answer:
0.095 is the probability that a randomly selected newborn baby is premature.
Explanation:
We are given the following information in the question:
Mean, μ = 266 days
Standard Deviation, σ = 16 days
We are given that the distribution of Pregnancy length is a bell shaped distribution that is a normal distribution.
Formula:
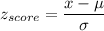
a) P(births that occur before 245 days)
P(x < 245)
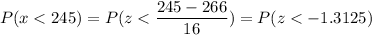
Calculation the value from standard normal z table, we have,

0.095 is the probability that a randomly selected newborn baby is premature.