Question

The length of needles produced by a machine has standard deviation of 0.01 inches. assuming that the distribution is normal, how large a sample is needed to determine with a precision of ±0.005 inches the mean length of the produced needles to 95% confidence?

Answer 1

Let X be the length of needle produced by machine. X follows Normal distribution with standard deviation σ=0.01

The margin of error ME = 0.005 and confidence interval is 95%

We have to find here sample size n from given information

The formula to find sample size when population standard deviation is known is

n =
`[(z_(\alpha/2) standard deviation)/(ME)] ^(2)`

where
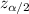`z_(\alpha/2)` is critical z value for 95% confidence interval

We have confidence level, c=0.95

α = 1- c = 1-0.95 = 0.05

α/2 = 0.05 /2 = 0.025

z (0.025) is z score value for which probability below -z is 0.025 and above z is 0.025

Using z score table to get z critical value

z = -1.96

For confidence interval calculation we use positive z score value 1.96

The sample size will be then

n =
`[(1.96 * 0.01)/(0.005)]^(2)`

n = 15.3664

Rounding sample size to nearest integer n=15

a sample is needed to determine with a precision of ±0.005 inches the mean length of the produced needles to 95% confidence is 15