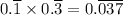There are a few different ways to convert repeating decimals into fractions. Going back to first principles, the usual trick is to get rid of the repeating part by subtracting the number from 10 times itself. (If it was six digits repeating we'd subtract from 10^6 times the number.)
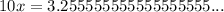
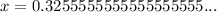
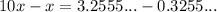
The repeating fives cancel and we're left with
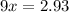
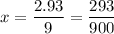
Once we do the trick a few times we see the denominator is always a series of nines followed by a series of zeros. The number of 9s is the period of repeat. The number of zeros is how many non-repeaters there are to the right of the decimal. So this would look more like:
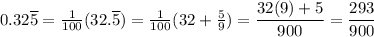
A purely repeating decimal is a geometric series, with a ratio that's a power of 10.

Once we learn to convert repeating decimals to fractions and back we think we understand them and we're done. But if you want to have some math fun, try to work out the algorithm for multiplication of repeating decimals. It's surprisingly difficult, but there is a trick. (No fair converting to fractions then back!).
For example, about the simplest multiplication of two repeating decimals is