Question

An airplane pilot can see the top of a traffic control tower at a 20 degree angle of depression. the airplane is 5,000 feet away from the tower horizontally. how far above the tower is the airplane? round to the nearest hundredth.

Answer 1

`y \approx 1819.851\,ft`

Explanation:

The vertical distance between the airplane and the traffic control tower is obtained by means of the following trigonometric relation:

`y = x \cdot \tan \theta`

`y = (5000\,ft)\cdot \tan 20^(\textdegree)`

`y \approx 1819.851\,ft`

Answer 2

The given question describes a right triangle with with one of the angles as 20 degrees and the side adjacent to the angle 20 degrees is of length 5,000 feet. We are looking for the length of the side opposite the angle 20 degrees.

Let the required length be x, then

`tan(20^o)=\cfrac{opp}{hyp}=\cfrac{x}{5,000}\\ \\ \Rightarrow x=5,000tan(20^o)=1,819.85`

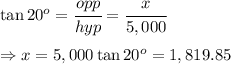
Therefore, the height of the airplane above the tower is 1,819.85 feet.