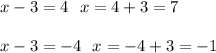"Isolate the constant by adding 7 to both sides of the equation."
This step separates the non-squareable 7 and the squareable
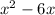
.
"Add 9 to both sides of
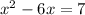
to form a perfect square trinomial while keeping the equation balanced."
After separating the non-squareable, add the number which makes the first or left side a perfect square trinomial. The formula to find the number is:
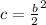
.
When we plug the values:
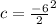
Simplify:

"Write the trinomial
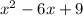
as

squared."
When you factor
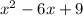
, you will get
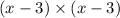
.
"Use the square root property of equality to get
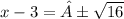
."
The 16 is coming from the part when we add 9. We needed 9 on the left side for a perfect square, but to protect the balance of the equality, we need to add 9 to the right side too. When we add 7 and 9, we got 16, and that is where it came from.
"Isolate the variable x to get solutions of -1 and 7."
To isolate x we branched the plus-minus sign: