Question

Given right triangle MUD such that mD = 23.1 and d = 38, which of the following statements are true? Round to the nearest hundredth. Check all that apply.

Answer 1

A. m=89.09 and B. u=96.06

Explanation:

Given the triangle MUD such that <D = 23.1° and d=38, we were ask which of the following statements are true, to know which statements are true, we need to check.

First lets check whether m = 89.09, to do this , we need to apply the trigonometric formula; SOH CAH TOA

Since we are dealing with angle D=23.1° then our adjacent will be m and our opposite will be d=38

adjacent = m

opposite =38

Using the trig formula;

tanФ = opposite / adjacent

tan23.1° = 38 / m

cross multiply

m tan23.1° = 38

Divide both-side by tan23.1°

m = 38 / tan23.1°

m = 89.08975

m=89.09 to the nearest hundredth

so, option A is true, m=89.09

If option A is true, then this makes option D is false; m≠18.92

Now, lets check option B

we are to find u

still using Ф = angle D, then hypotenuse = u and opposite =d=38

opposite = 38

hypotenuse = u

Using trig. formula;

sinФ = opposite / hypotenuse

sin 23.1° = 38 / u

cross multiply

u sin23.1° = 38

divide both-side of the equation by sin 23.1°

u = 38 / sin23.1°

u = 96.855

u = 96.86 to the nearest hundredth

This makes option B to be true

Now, we proceed to check option C

We need to find angle M

since, our angle is now M, the our adjacent will now be d=38 and opposite will be m=89.09

adjacent = 38

opposite = 89.09

Using trig. formula;

tanФ = opposite / adjacent

tan M = 89.09 / 38

tan M = 2.34447

To get the value of M, we take the
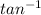`tan^(-1)` of both-side

M =
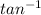`tan^(-1)` (2.34447)

M = 66.9°

Therefore <M =66.9°