Answer:
The correct option is B)
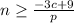 .
.
Explanation:
Consider the provided inequality:
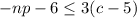
Now distribute 3 inside the parentheses.
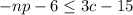
Add 6 on both the side of the inequality:

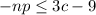
Now, multiply both the sides by a negative sign and reverse the sign of inequality.
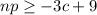
Divide both the sides of the inequality by p.
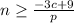
Now consider the provided options.
By observing the provided option it can be concluded that the correct option is B)
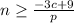 .
.