Hey there!
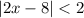
This equation is a "and" problem
So, add
 to both of your sides!
to both of your sides!

We get:
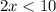
Divide by
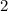 to your sides
to your sides
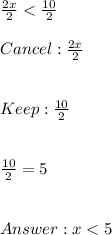
Or you can use this add this part to your equation because this is a two step inequality
Add
 to your sides again
to your sides again

We get:
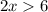
Divide by
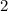 on each of your sides
on each of your sides

Answer:
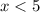 and
and
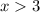
Overall answer:
Good luck on your assignment and enjoy day!
~