Question

What is the value of the expression i0•i1•i2•i3•i4

-1

1


i


-i

Answer 1

I hope you are trying to write

`i^0*i^1*i^2*i^3*i^4`

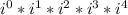
Now,
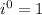`i^0=1` Because any number to exponent 0 always result 1.

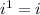`i^1=i` Any number to exponent 1 will result the same number.

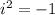`i^2= -1` By using the property of imaginary number.

`i^3= i^2*i =(-1)*i= -i`

`i^4=i^2*i^2=(-1)*(-1)=1`

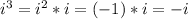
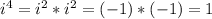
Now we can plug in these values in the given expression to get the value of the expression. So,

`i^0*i^1*i^2*i^3*i^4`

=
`1*i*(-1)*(-i)*1`

=
`i^2`

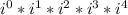
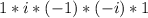
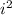
=-1

So, -1 is the correct choice.

Answer 2

`\bf \stackrel{1}{i^0}\cdot \stackrel{i}{i^1}\cdot \stackrel{-1}{i^2}\cdot \stackrel{-i}{i^3}\cdot \stackrel{1}{i^4}\implies i\cdot i\cdot 1\implies i^2\implies -1`