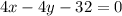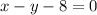Question

The point nearest to the origin on a line is at (4, -4). Find the standard form of the equation of the line.

Answer 1

Just did a specific one of these; let's do the general case.

The point nearest the origin is (a,b).

The line from the origin through the point is

`bx - ay = 0`

The line we seek is perpendicular to this one. We swap the coefficients on x and y, negating one, to get the perpendicular family of lines. We set the constant by plugging in the point (a,b):

`ax + by = a^2 + b^2`

`ax + by -( a^2 + b^2) = 0`

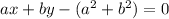
That's standard form; let's plug in the numbers:

`4 x - 4 y - 32 = 0`

`x - y - 8 = 0`