Classic Algebra and its unnecessarily complicated sentence structure. As you may have probably known, Algebra has its own "vocabulary set".
"the length of a rectangle exceeds its width by 6 inches" -> length is 6 in. longer than width -> l= w + 6
Since we're solving for the length and width, let's give them each variables.
length = l = w+6
width = w
The next bit of information is "the area is 40 square inches"
Applying the formula for the area of a rectangle we can set up:
l x w = 40
replace "l", or length, with it's alternate value.
(w+6) x w = 40
distribute
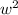 + 6w = 40
+ 6w = 40
subtract 40 from both sides
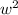 + 6w - 40 = 0
+ 6w - 40 = 0
factor
(w - 4)(w + 10) = 0
solve for w
w= 4, or -10
So great, we have 2 values; which one do we choose? Since this problem is referring to lengths and inches, we will have to choose the positive value. There is not such thing as a negative distance in the real world.
We now have half of the problem solved: width. Now we just need to find the length which we can do but substituting it back into the original alternate value of l.
l = w + 6
w=4
l = 4 + 6 = 10
The length is 10 in. and the width is 4 in. Hope this helps!