1)
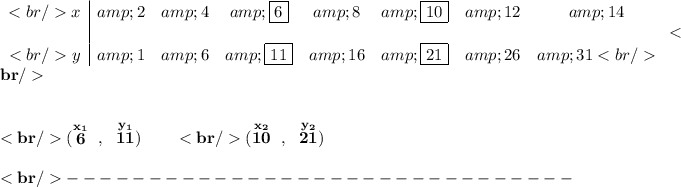
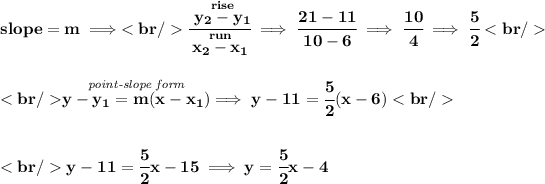
2)
well, for radical with an even root, like the square root with a root of 2, it can't have a negative radicand.
so 3√(x-2) the x-2 part must never become negative, if it ever does, then you'd get an imaginary root or so-called complex root, which is another way of saying no real root for such radicand.
and for x-2 that occurs if x ever becomes less than 2. if x is 2, then we get 2-2 =0, and 0 is ok, but something like 1-2 = -1, and √-1 is just "i", and if we go down further, say x = -5, then we get -5-2 = -7 and √-7 is just i√7, yet another imaginary root.
so the restriction is that x can never become less than 2.
therfore, the domain is in Set Builder form x ∈ ℝ, x ⩾ 2 .