Question

Help binomial distributions

Answer 1

We have the formula to compute the probability of having exactly k successed over n trials, given a probability p of success (and implicitly a probability 1-p of failure), which is

`P(\text{k successed on n trials}) = \binom{n}{k}p^k(1-p)^(n-k)`

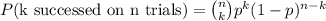
Now, the probability of at least 3 successes is the union of the following event: exactly three successes,exactly four successes and exactly five successes.

We can compute their probability and sum them:
`\binom{5}{3}\left((3)/(7)\right)^3\left((4)/(7)\right)^2 + \binom{5}{4}\left((3)/(7)\right)^4\left((4)/(7)\right)^1 + \binom{5}{5}\left((3)/(7)\right)^5 \approx 0.36788`

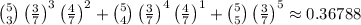
So, the answer is about 36.79%