Question

Line segment GT contains the point G(−3, 5) and a midpoint at A(1, −4). What is the location of endpoint T?

Answer 1

Imagine you're moving along the segment. Since the midpoint is in the middle of the segment (obviously), it means that when you've traveled from G to A, you're halfway through your journey, along both x and y directions. So, let's break the problem in two and analyze both directions.

Along the x axis, you've moved from -3 to 1, so you moved 4 units forward. This means that you have 4 units still to go, and your journey will end at coordinate 5.

Similarly, along the y axis, you've moved from 5 to -4, so you moved 9 units downward. This means that you have 9 units still to go, and your journey will end at coordinate -13.

So, the coordinates of the endpoint are
`T = (5,-13)`

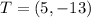
If you prefer a more analyitical approach, simply write the definition of the midpoint and solve it for the coordinates of T.

We have
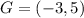`G = (-3, 5)` and
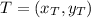`T = (x_T,y_T)`. The midpoint is computed as

`A = \left( (-3+x_T)/(2),(5+y_T)/(2) \right) = (1, -4)`

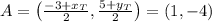
So, you have the equations

`(-3+x_T)/(2) = 1,\qquad (5+y_T)/(2) = -4`

Multply both equations by 2 to get

`-3+x_T = 2,\qquad 5+y_T = -8`

Move the constants to the right hand sides to get

`x_T = 5,\qquad y_T = -13`