A particle is moving along a projectile path where the initial height is 160 feet with an initial speed of 144 feet per second. What is the maximum height of the particle? Hint:…

Question

asked Aug 8, 2019 133k views

1 Answer

Aboyko · Answer 1 · 2019-08-14T05:41:16+0000

Answer:

D) 484 feet

Explanation:

Given:
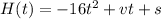H(t) = -16t^2 + vt + s , where t is the time, v is the initial velocity/speed and s is initial height.

and

v = 144 feet and s = 160 feet

Now plug in the given values in the given
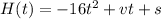
H(t) = -16t^2 + vt + s

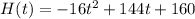
H(t) = -16t^2 + 144t + 160

This is in the form of quadratic function
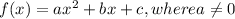
$f(x) = ax^2 + bx + c, where a \\eq 0$

The maximum height attain in vertex. Here we have formula to find the vertex of the x coordinate.

x =
(-b)/(2a)

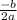
Here b = 144 and a = -16

So, t =
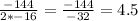
(-144)/(2*-16) = (-144)/(-32) = 4.5

The maximum height attain at t = 4.5 seconds. To find the maximum height plug in t = 4.5 in
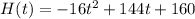
H(t) = -16t^2 + 144t + 160

H(4.5) =
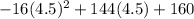
$-16(4.5)^2 + 144 (4.5) + 160\\$

= -16(20.25) + 648 + 160

= -324 + 648 + 160

= -324 + 808

= 484 feet

So the maximum height of the particle is 484 feet.