Question

Hot dogs come in packages of 10 and hot dog buns come in packages of 8 . What is the least amount of product that you need to Buy if you want exactly One hot dog for each hot dog bun

Answer 1

The lowest amount of hot dog packages you would need to buy is 4, and the lowest amount of hot dog bun packages you would need to buy is 5. This would leave you with 40 hot dogs in total.

To answer this question, you need to find the lowest common multiple of 10 and 8. You can do this by first finding the prime factors of 10 and 8, so:

10 -> 5 × 2
8 -> 2 × (4) -> 2 × 2

Now you multiply together all of the prime numbers, so you get 5 × 2³ as both factors share one 2, and 10 has a 5 and 8 has an extra two 2's.

2³ = 8, and 5 × 8 = 40, so you will end up with 40 total hot dogs and buns.

To find the amount of packages needed, you simply need to divide 40 by the amount that is in each package, so 40 ÷ 10 = 4, and 40 ÷ 8 = 5.

I hope this helps!

Answer 2

This exercise is solved by finding the least common multiple between 10 and 8.

In fact, you have to buy a certain number
`h` of hot dog package, and you will have
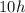`10h` hot dogs, since there are 10 hot dogs in each package. The key concept here is that the number of hot dogs you have in the end is a multiple of the number of hot dogs in each box.

Similarly, you have to buy a certain number
`b` of hot dog buns package, and you will have
`8b` hot dogs, since there are 8 hot dog buns in each package. Again, the key concept here is that the number of hot dog buns you have in the end is a multiple of the number of hot dog buns in each box.

Then, you want to have the same number of hot dogs and hot dog buns, i.e. you want

`10h = 8b`

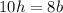
but you also want
`h` and
`b` to be the first values to satisfy this equation.

This means that you want a multiple of 10 to equal a multiple of 8, and you want the smallest possible number which does the trick. Again, this is exactly the definition of the least common multiple.

To find the least common multiple of two numbers, find their prime factorization, and collect all the primes from both factorizations, with the highest exponent possible. Since
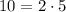`10 = 2\cdot 5` and
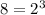`8 = 2^3`, the primes appearing are 2 and 5. The higher exponent for 2 is 3, and the only exponent for 5 is 1. So, the answer is
`2^3\cdot 5 = 40`.

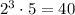So, if you buy 4 packages of hot dogs and 5 packages of hot dog buns, you will have 40 hot dogs and 40 hot dog buns, as requested.