The answer is
First of all, note that we can solve all angles, since we have
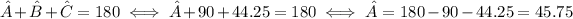
where
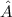 is the angle centered in vertex A, and so on.
is the angle centered in vertex A, and so on.
Now we can use the law of sines, which states that the ratio between a side and the sine of the opposite angles is constant.
So, you would have
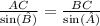
plug in the known values:
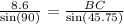
Since sin(90)=1, the denominator of the first fraction disappears. Finally, we can solve for BC:
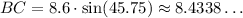
Which gives 8.43 when rounded as required.