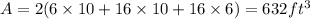Question

You are designing a miniature golf course and need to calculate the surface area and volume of many of the objects that will be used to build the course.

a. The first hole has a sphere that has a radius of 5 feet. What is the surface area and volume of the sphere?
b. The fourth hole has a pyramid that has a height of 12 feet; the base is a square with sides that measure 8 feet. What is the surface area and volume of the pyramid?
c. The seventh hole has a cone that has a height of 8 feet; the base has a radius of 5 feet. What is the surface area and volume of the cone?
d. The fourteenth hole has a rectangular solid that measures 10 feet long, 6 feet wide, and 16 feet tall. What is the surface are and volume of the rectangular solid? e. Your boss wants to place signs on each face of the structures. How many faces are on the four geometric shapes on the holes?
f. To meet building codes we need to know the number of edges to place the appropriate bracket

Answer 1

a. We know that the volume of a sphere is given by
`V=(4)/(3)\pi r^(3)`.

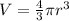Therefore, volume of the sphere with radius, r=5 feet will be:

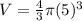`V=(4)/(3)\pi (5)^(3)`=523.6
`ft^3`.

We also know that the formula for the surface area of a sphere is given by:

`S=4\pi r^(2)`

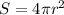
Therefore, surface area of the sphere of radius r=5 feet will be:

`S=4\pi (5)^(2)=314.16 ft^2`

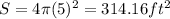
b. We know that the volume of a pyramid is given by
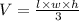`V=(l* w* h)/(3)`, where h is the height which is 12 feet and w and l are the width and the length of the base which in this case are each equal to 8 feet. So, the volume of the pyramid will be:

`V=(8* 8* 12)/(3)=256 ft^3`.

We also know that the formula for the surface area of the pyramid is:

`S=lw+l\sqrt{((w)/(2))^(2)+h^(2)}+w\sqrt{((l)/(2))^(2)+h^(2)}`

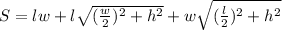
After plugging in the given values we get:

`S=8*8+8\sqrt{((8)/(2))^(2)+12^(2)}+8\sqrt{((8)/(2))^(2)+12^(2)}\approx 266.4`

c. For a Cone we know that the volume is given by
`V=(1)/(3)\pi r^(2)h`

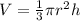
We know that the height, h of the cone is 8 feet and the radius of the base of the cone, r is 5 feet. If we plug in these values we will get:

`V=(1)/(3)\pi * 5^(2)*8\approx209.4 ft^(3)`

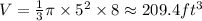
Likewise, the surface area of the cone is:

`A=\pi r(r+\sqrt{h^(2)+r^(2)})`

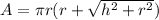
After plugging in the values we will get, the value of the surface area as

`A=\pi * 5(5+\sqrt{8^(2)+5^(2)})\approx226.7 ft^(2)`

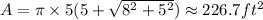
d. The fourteenth hole has a rectangular solid. Its height, h is 16 feet. Width, w is 6 feet and length, l is 10 feet.

The formula for the volume of such rectangular solid is:
`V=lwh`

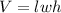
Plugging in the value gives
`V=10*6* 16=960 ft^(3)`

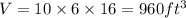
Likewise, the Surface Area formula is given by:

`A=2(wl+hl+hw)`

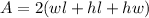
Plugging in gives:
`A=2(6*10+16*10+16*6)=632 ft^(3)`