Question

PLEASE ANSWER ASAP

Suppose that a company claims that its batteries last 245 hours on average. It took many large samples, and each time the mean number of hours was outside the 95% confidence interval. Based on this information alone, which of the following is probably not the mean number of hours that the company's batteries last? A.)240 B.)235 C.)230 D.)245

Answer 1

The correct answer is D: 245

Answer 2

The correct option is D.

Explanation:

Confidence interval is used to express the degree of uncertainty associated with a sample statistic.

The confidence interval is calculated as,

`\mu\pm z\cdot (\sigma)/(√(n))`

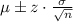
The value of z score at 95% confidence interval is 1.96.

The confidence interval for given information is

`245\pm 1.96\cdot (\sigma)/(√(n))`

It is given that in each time of sampling the mean number of hours was outside the 95% confidence interval. It means σ can not be zero.

`\sigma\\eq 0`

`(\sigma)/(√(n))\\eq 0`

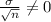
It means the mean number of hours that the company's batteries last will be either below or above 245.

Therefore, the value can be anything, but not 245. The correct option is D.