Answer:
Givens:
Using this information we could recur to SAS postulate to demonstrate the congruence of this pair of triangles. We already have one side and one angle congruent, we just need to demonstrate that
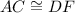 , that will prove the complete congruence.
, that will prove the complete congruence.
So, based on the given coordinates, we're able to calculate the length of each side and find if they are the same. We use this formula:

Therefore,
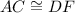 , because they have the same length.
, because they have the same length.
Now, based on these congruences:
We demonstrate by the Side-Angle-Side (SAS) postulate that ΔABC ≅ ΔDEF.