Question

A random sample of 140 students is chosen from a population of 3,500 students. If the mean IQ in the sample is 105 with a standard deviation of 9, what is the 95% confidence interval for the students' mean IQ score?

answer options:

A. 100-120

B.107.9-112.1

C. 103.5-106.5

D.108.66-11.34

Answer 1

103.5–106.5

Explanation:

just took the test

Answer 2

Given : Sample size n=140, sample mean m = 105 and sample standard deviation s=9

We have to find 95% confidence interval for population mean which is given by

(m - Margin of error ) ≤ μ ≤ (m + Margin of error)

Where Margin of error is given by

Margin of error =
`(s*t)/(√(n))`

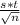
Where t = t critical value at alpha/2 level of significance and (n-1) degrees of freedom

Here alpha = 1- c = 1-0.95 = 0.05

degrees of freedom = n-1 = 140-1 = 139

Here we will use excel function to find t critical value which is

T.INV.2T(0.05, 139) = 1.977

The margin of error will be

ME =
`(9 * 1.977)/(√(140))`

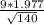
ME = 1.5

The 95% confidence interval will become

(105 - 1.5 , 105 + 1.5)

(103.5, 106.5)

So the correct answer option is option C. (103.5, 106.5)