Answer : (1, 4.4) and (1, 11.6)
Equation of ellipse is
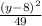 +
+
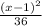 = 1
= 1
From the equation we know that center (h, k) is (1,8)
The equation is in the form of
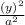 +
+
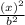 = 1
= 1
a^2= 49 so a= 7
b^2 = 36 so b= 6
To find foci , we find the distance between the center of ellipse and foci that is represented as C
We know c^2 = a^2 - b^2
Plug in the values
c^2 = 7^2 - 6^2
c^2 = 49 - 36= 13
So c= sqrt(13)= 3.61
Foci = (h, k +c) and (h, k-c)
We know h=1, k=8 and c= 3.61
(h, k+c) = (1, 8+3.61) = (1, 11.6)
(h, k-c) = (1, 8 - 3.61)= (1, 4.4)
So foci = (1, 4.4) and (1, 11.6)